в точках расположения масс m1
Прикладываем поочередно силу



Путем перемножения соответствующих эпюр способом Верещагина вычисляем единичные перемещения:


Частотный определитель:

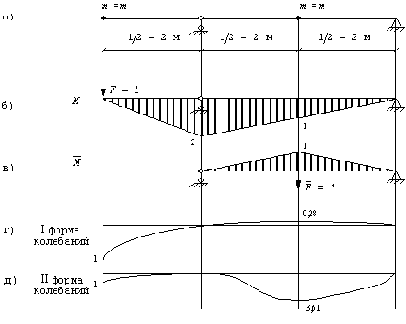
Рис. 29
или

где

Частотное уравнение:

Собственные частоты колебаний:

Система алгебраических уравнений относительно амплитуд колебаний А1 и А2:

Полагая А1=1, находим А2 из первого уравнения системы сначала при



Формы колебаний представлены на рис. 29,г,д.
Проверяем выполнение условия ортогональности:

Пример 8. Определитель частоты свободных колебаний балки с тремя равными сосредоточенными массами m (рис. 30,а), если m=0,5



Решение
Так как система и расположенные на ней массы симметричны, то задача может быть решена с использованием симметрии.
Строим единичные эпюры изгибающих моментов

(рис. 30,б,в,г).
Вычисляем единичные перемещения путем перемножения соответствующих эпюр по способу Верещагина:
.
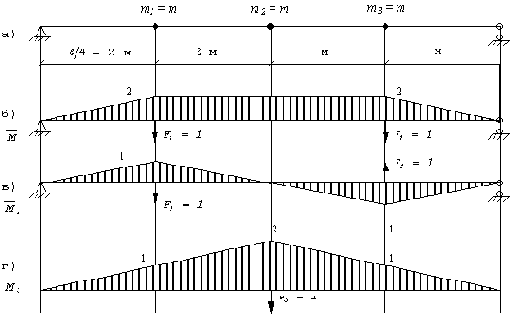
Рис. 30

Определитель для симметричных колебаний составляем с учетом того, что перемещения от групповой силы


или

Соответствующее частотное уравнение:

Собственные частоты симметричных колебаний:

Частотное уравнение для обратно симметричных колебаний:


Пример 9. Определить собственные частоты и формы колебаний системы, состоящей из трех дисков с моментами инерции масс


Уравнения движения системы, составленные прямым методом, таковы:

Решение системы ищем в виде

После подстановки получаем систему однородных алгебраических уравнений:

Приравнивая определитель системы нулю и раскрывая его, получим частотное уравнение

Собственные частоты колебаний:

Нулевая частота соответствует повороту вала и дисков как жесткого целого.
Для ненулевых частот определяем собственные формы колебаний, принимая А2 = 1.
Соотношение между амплитудами:

Первая форма колебаний при


Вторая форма колебаний при


Пример 10. Методом последовательных приближений определить две низших частоты собственных колебаний судовой дизельной установки по уточненной схеме, состоящей из дисков 1-6, к которым приведены кривошипы двигателей, маховика 7 и гребного винта 8 с присоединенными массами гребного вала и воды (рис.31,а) при следующих данных:

Значения частот в первом приближении определить для упрощенной трехдисковой схемы (рис. 31,б).

Рис. 31
Для приближенного определения двух низших частот образуем упрощенную схему (рис.31,б), в которой первые шесть дисков заменены одним общим, причем

Длина участка


Таблица 1
|
№ диска |
I |
 |
A |
 |
 |
C |
 |
|
1 |
0,28 |
144,48 |
1,000 |
144,48 |
144,48 |
2.104 |
0,007 |
|
2 |
0,28 |
144,48 |
0,993 |
143,47 |
287,95 |
2.104 |
0,014 |
|
3 |
0,28 |
144,48 |
0,979 |
141,45 |
429,40 |
2.104 |
0,021 |
|
4 |
0,28 |
144,48 |
0,958 |
138,34 |
567,74 |
2.104 |
0,028 |
|
5 |
0,28 |
144,48 |
0,930 |
134,31 |
702,05 |
2.104 |
0,035 |
|
6 |
0,28 |
144,48 |
0,895 |
129,29 |
831,34 |
2.104 |
0,042 |
|
7 |
8,4 |
4334,4 |
0,853 |
3699,12 |
4530,46 |
1,2.103 |
3,775 |
|
8 |
3,0 |
1548,0 |
-2,922 |
-4523,85 |
6,61 |

Приближенные значения двух низших частот:

В качестве первого приближения для уточнения первой собственной частоты колебаний принимаем

Полученное значение остатка



Таблица 2
|
№ диска |
I |
 |
A |
 |
 |
C |
 |
|
1 |
0,28 |
148,4 |
1,000 |
148,4 |
148,4 |
2.104 |
0,007 |
|
2 |
0,28 |
148,4 |
0,993 |
147,3 |
295,7 |
2.104 |
0,015 |
|
3 |
0,28 |
148,4 |
0,978 |
145,2 |
440,9 |
2.104 |
0,022 |
|
4 |
0,28 |
148,4 |
0,956 |
141,9 |
582,8 |
2.104 |
0,029 |
|
5 |
0,28 |
148,4 |
0,927 |
137,6 |
720,4 |
2.104 |
0,036 |
|
6 |
0,28 |
148,4 |
0,891 |
132,2 |
852,6 |
2.104 |
0,043 |
|
7 |
8,4 |
4452,0 |
0,848 |
3776,9 |
4629,5 |
1,2.103 |
3,858 |
|
8 |
3,0 |
1590,0 |
-3,01 |
-4785,8 |
-156,3 |
Частотное уравнение (75) после подстановки в него заданных числовых значений принимает вид

Собственные частоты:

Для определения собственных форм колебаний воспользуемся формулой (76)

Собственные формы колебаний представлены на рис. 34,а,б.
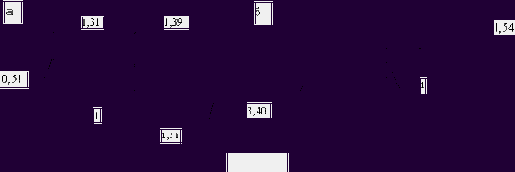
Рис. 34
Первая форма представляет собой, в основном, «подпрыгивание» кузова, а вторая - «галопирование».
Убедимся в ортогональности этих форм. Условие ортогональности имеет вид

Частота возмущающей силы:

При наступлении резонанса


отсюда находим длину балки при резонансе:

Для выполнения условия


Амплитуда вынужденных колебаний:

где


Статический прогиб от собственного веса двигателя:

Статическое напряжение:

Динамический коэффициент:

Динамическое напряжение:

Пример 13. К валу переменного сечения с жёстко заделанными концами прикреплён маховик, на который действует переменный момент





а
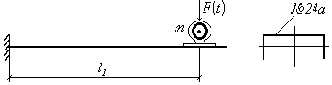
б
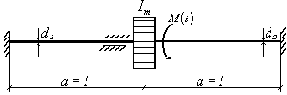
Рис. 46
Жёсткость вала:

Собственная частота колебаний:

Угол поворота маховика от действия момента, равного амплитуде возмущающего момента:

Амплитуда колебаний:

Соответствующий динамический момент:

Максимальные касательные напряжения в левой и правой частях вала:

Пример 14. Вдоль пути синусоидального профиля


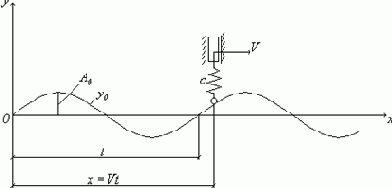
Рис. 47
Подставляя в уравнение профиля пути


Обозначая через у абсолютное вертикальное перемещение груза, отсчитываемое от равновесного уровня, дифференциальное уравнение движения запишем в виде

или

Отсюда следует, что эквивалентная вынуждающая сила

т.е. её амплитуда равна

Амплитуда абсолютных колебаний груза:

По условиям задачи


тогда
c <

Пример 15. Двигатель весом 2,4 т установлен на десяти одинаковых пружинах диаметром




Отношение


Частота возмущающей силы:

Необходимое значение собственной частоты:

Необходимая жёсткость всех пружин:

Число витков:

Следует принять, по крайней мере, 17 витков, так как увеличение числа витков снижает жёсткость системы и уменьшает динамический коэффициент. Если принять

Пример 16. На двух балках посередине пролёта установлен двигатель массой






Приведенная масса системы:

где

Собственная частота колебаний:

Принимая


Статический прогиб от амплитудного значения возмущающей нагрузки:


Амплитуда колебаний:

Статический прогиб:

Статическое напряжение:

Динамическое напряжение:

Уравнение движения масс:

Решение уравнений ищем в виде

После подстановки получим систему алгебраических уравнений

Единичные эпюры моментов, необходимые для вычисления коэффициентов

Перемножая соответствующие эпюры по способу Верещагина, получим значения перемещений


Частота вибрационной нагрузки:

После подстановки в систему алгебраических уравнений находим амплитуды колебаний:

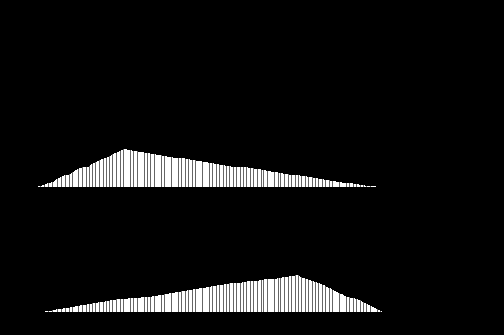
Рис. 53
Соответствующие динамические нагрузки


Так как А1 и А2 близки по величине, то

тогда

С учетом статической нагрузки находим

Максимальное напряжение в балках:

Пример 18. Построить эпюру динамических изгибающих моментов для невесомой балки пролетом l = 4м при действии возмущающей силы



Решение.
Опуская вид единичных эпюр(см. пример 7), приведем значения перемещений




Эпюра от амплитудного значения возмущающей силы показана на рис.54,б.
Перемножая эпюру





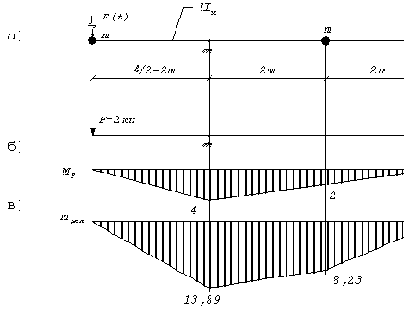
Рис. 54
Собственные частоты колебаний балки вычислены ранее (пример 7) и равны:

«Исправленные» главные перемещения:

Система канонических уравнений динамического варианта метода сил для вычисления сил инерции X1 и X2 имеет вид:

После подстановки числовых значений коэффициентов получим:

Силы инерции:

Используя формулу:

строим эпюру динамических изгибающих моментов Mдин (рис.54,в).
Пример 19. Построить эпюру динамических изгибающих моментов в симметричной раме (рис.55,а) при действии на нее симметричной динамической нагрузки



Решение.
Так как вибрационная нагрузка симметрична, то формы вынужденных колебаний также будут симметричными. Групповые симметричные неизвестные силы инерции показаны на рис.55,б. Эпюры моментов от единичных сил


Точное значение низшей частоты такой консоли вычислено Кирхгофом в виде

Для приближенного решения принимаем

Каждый член этого разложения удовлетворяет граничным условиям задачи



Если ограничиться одним членом разложения, то по методу Рэлея

при этом ошибка составляет около 3 %.
Чтобы получить лучшее приближение, возьмем два члена разложения, подставив их в (274),

Дифференцируя это выражение по С1 и С2 поочередно, приходим к системе уравнений

Приравнивая нулю определитель, составленный из коэффициентов этих уравнений, получим частотное уравнение, меньший корень которого

что даёт ошибку 0,1 %.