Свободные колебания системы с одной степенью свободы без трения

В большинстве упругих систем при достаточно малых перемещениях сила упругости линейно зависит от перемещения x. Если начало отсчёта смещения x выбрать так, что при x=0: F=0, то для линейной системы F = cx, где с - коэффициент жесткости системы.

Дифференциальное уравнение движения системы с одной степенью свободы (рис. 11,а) таково: 

.                                                (4)

Вид дифференциального уравнения не меняется при действии на систему постоянных сил (например, сил тяжести), если смещение тела отсчитывать от положения его статического равновесия.

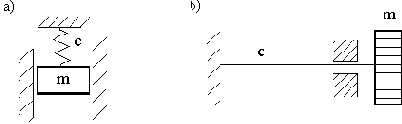
Рис. 11

Действительно, уравнение движения тела массой m (рис.11,а), находящегося под действием силы тяжести и совершающего свободные колебания, имеет вид

  

,                                            (5)

где

- удлинение пружины от силы тяжести груза.

Следовательно, слагаемые mg и cfст в уравнении (5) взаимно уничтожаются, и уравнение (5) совпадает с (4).

Уравнение движения одномассовой системы, совершающей крутильные свободные колебания (рис. 11,б), записывается аналогично:

  

,

где

 - угол поворота тела; J- момент инерции массы m относительно продольной оси вала; с - крутильная жесткость упругой связи.

Решение уравнения (4) имеет вид

  

,                                            (6)

где

- угловая частота колебаний, или собственная частота; С1 и С2- постоянные интегрирования, определяемые из начальных условий.

Обозначая смещение и скорость в начальный момент времени t0=0 через x0 и

 соответственно, после подстановки в (6) находим

  

 , .                                              (7)

   Выражение (6) можно записать иначе:

  

,                                              (8)

где

,

 .

Таким образом, движение груза при свободных колебаниях одномассовой системы без трения описывается синусоидальным законом с амплитудой колебаний А, периодом

 и начальной фазой  (рис.12).

Период колебаний

 определяется из условия:

  

,

откуда

  

 .                                              (9)

Число колебаний в единицу времени (техническая частота, измеряемая в герцах):

.                                                  (10)



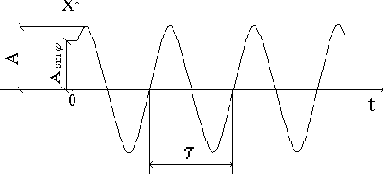
Рис. 12

В практическом отношении иногда оказывается удобным связать частоту и период колебаний со статической деформацией fст  упругой связи, вызванной силой, равной весу груза, .

При этом справедливы формулы:

    ;   ;  .                              (11)

Так как величина fст  введена в (11) формально, то очевидна их справедливость независимо от того, совпадает или не  совпадает направление силы тяжести с направлением движения груза.

Для анализа свободных колебаний удобно использовать изображение закона движения системы на фазовой плоскости, или так называемый фазовый портрет. Фазовым портретом движения называется графическое изображение зависимости скорости движения от смещения. Для получения фазового портрета продифференцируем выражение (8) по t:

                                            (12)

Уравнение движения (8) и выражение (12) представляют собой уравнение фазовой траектории в параметрической форме. Исключая параметр , получим

   .                                             (13)

Уравнение (13) является уравнением эллипса с полуосями, равными А и  (рис. 13,а). Верхняя полуплоскость соответствует возрастанию смещения, нижняя - убыванию. Размеры эллипса зависят от начальных условий, определяющих амплитуду колебаний А.



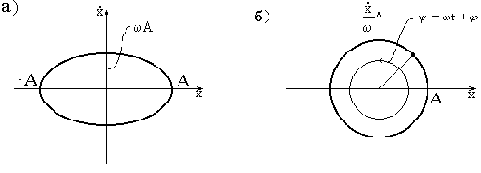
Рис. 13

Все возможные свободные колебания одномассовой системы изображаются семейством эллипсов, каждый из которых соответствует определённому уровню энергии. Чем больше амплитуда колебаний А, тем больше полная энергия системы. Если значения энергии откладывать по оси , перпендикулярной чертежу, то получится поверхность (параболоид), нижняя точка которой соответствует нулевому энергетическому уровню. Точка, изображающая значения смещения и скорости в данный момент времени (изображающая точка), перемещается по горизонтали этой поверхности.

Если изменить масштаб построения фазовой траектории и откладывать по оси абсцисс х, а по оси ординат - , то фазовая траектория (рис. 13,б) будет представлять собой окружность радиусом А, причём изображающая точка будет равномерно двигаться по этой окружности с угловой скоростью, равной частоте собственных колебаний .

   При наличии рассеяния энергии изображающая точка перемещается по спирали, приближаясь к началу координат.


Содержание раздела

---

---