Сухое трение
Рассмотрим движение упруго закрепленного тела массой m по шероховатой поверхности. Как уже отмечалось, в этом случае говорят, что имеет место сухое трение (рис.17). Сила трения, действующая на массу m, постоянна по величине и направлена в сторону, противоположную движению. Уравнение свободных колебаний такой системы имеет вид

где знак плюс соответствует этапу движения, на котором скорость положительна, а знак минус - этапу движения, на котором скорость отрицательна.
Зависимость полной действующей на груз силы F=cx

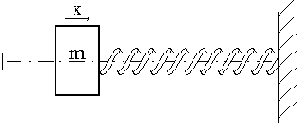
Рис. 17
Перепишем уравнение (24) в виде

Функция sgn






Уравнение (25) содержит нелинейное слагаемое. Тем не менее можно найти решение, если рассмотреть последовательные интервалы движения, на каждом из которых скорость
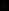
Отклоним массу m в крайнее правое положение на величину А и отпустим ее без начальной скорости. В этом случае
x0=A ;

Под действием натяжения пружины на этом этапе груз двигается влево (
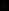

или

где


Коэффициент а представляет собой отклонение груза под действием максимально возможной силы трения. При отклонении массы m на величину, меньшую или равную а, движение не начнётся, так как силы упругости пружины недостаточно для преодоления силы трения. Полоса -а<x<a называется зоной застоя. Поэтому уравнение (27) имеет место при А>a.
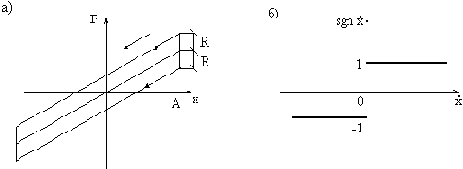
Рис. 18
Общее решение уравнения (27) имеет вид

Определяя постоянные интегрирования из начальных условий (26) получим

Закон движения (28) справедлив до тех пор, пока
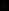


В этот момент масса m остановится, смещение x равно

т. е. под влиянием трения отклонение массы m уменьшилось по абсолютной величине на 2а.
После остановки масса m начнёт двигаться вправо. Повторяя приведенные выше расчёты, можно показать, что движение слева направо также продолжается в течение времени

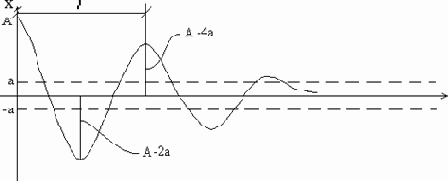
Рис. 18*
Время


Наличие сухого трения не меняет частоту колебаний.
Фазовый портрет свободных колебаний системы с сухим трением представлен на рис.19.
В координатах

Если в (27) ввести новую переменную









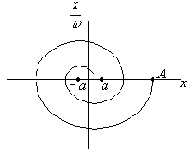
Рис. 19