Основное уравнение
Из курса сопротивления материалов известны дифференциальные зависимости при изгибе балок:


где EJ - жёсткость при изгибе; y=y(x, t) - прогиб; M=M(x , t) - изгибающий момент; q - интенсивность распределённой нагрузки.
Объединяя (189) и (190), получим

В задаче о свободных колебаниях нагрузкой для упругого скелета являются распределённые силы инерции:

где m - интенсивность массы балки (масса единицы длины), и уравнение (191) принимает вид

В частном случае постоянного поперечного сечения, когда EJ = const, m = const, имеем:

Для решения уравнения (192) полагаем, как и выше,
y = X (x)× T (t). (193)
Подставляя (193) в (192), приходим к уравнению:

Для тождественного выполнения этого равенства необходимо, чтобы каждая из частей равенства была постоянной. Обозначая эту постоянную через



Первое уравнение указывает на то, что движение носит колебательный характер с частотой

Второе уравнение определяет форму колебаний. Решение уравнения (195) содержит четыре постоянных и имеет вид

где

Удобно использовать вариант записи общего решения, предложенный А.Н.Крыловым:

где

представляют собой функции А.Н.Крылова.
Обратим внимание на то, что S=1, T=U=V=0 при x=0. Функции S,T,U,V связаны между собой следующим образом:
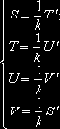
Поэтому производные выражения (197) записываются в виде

В задачах рассматриваемого класса число собственных частот


Для определения собственных частот и формул необходимо рассмотреть граничные условия.