Оптимизация регулируемого электропривода с упругими связями по критерию минимума колебательности
Рассмотрение физических свойств регулируемого электропривода с обратными связями по моменту (току) и скорости и его оптимизация инженерным методом последовательной коррекции по критериям точности, быстродействия и качества регулирования были выполнены в предположении, что полученные в §1.5 условия допустимости пренебрежения влиянием упругих механических связей выполняются. Однако возрастающие в процессе развития техники требования к точности воспроизведения заданных законов движения электропривода и к ограничению динамических нагрузок приводимых в движение машин постоянно расширяют круг промышленных объектов, в которых выполнение этих требований без учета влияния упругих механических связей недопустимо.
Возможность демпфирования электроприводом упругих колебаний в механической части, рассмотренная в §4.6, сегодня широко используется на практике. Как показано в §4.6 при заданных параметрах механической части колебательность двухмассовой упругой электромеханической системы, не замкнутой внешними обратными связями, определяется динамической жесткостью механической характеристики электропривода. Простейшим путем введения в силовую цепь двигателя добавочных резисторов и соответствующего изменения жесткости достигается изменение демпфирования, улучшение качества динамических процессов в механизме. Введение обратной связи по моменту (току), как показано в гл.7, позволяет при определенных условиях достигать того же эффекта без дополнительных потерь энергии. Наконец, в данной главе рассмотрены широкие возможности изменения жесткости механических характеристик с помощью обратной связи по скорости. Выбор жесткости при проектировании только из условия точности регулирования скорости без учета влияния упругих механических связей на колебательность системы может приводить к созданию неточных, ненадежных или практически неработоспособных установок.
Таким образом, вопросы анализа и синтеза упругих электромеханических систем регулируемого электропривода имеют исключительно важное практическое значение.
Для специалиста- электроприводчика анализ свойств упругих систем облегчает проектирование и наладку электроприводов, а инженерные методы синтеза позволяют решать задачи оптимизации регулируемых электроприводов с упругими механическими связями по различным критериям. Наиболее часто требуется реализация максимальной демпфирующей способности электропривода, поэтому ограничимся рассмотрением оптимизации по критерию минимума колебательности упругих электромеханических систем, замкнутых обратными связями по координатам первой массы: по моменту (току), скорости двигателя, их производным и т.п.
Сравнив структурные схемы на рис.7.12, 7.22, 8.11, 8.14, 8.20,в, 8.21, можно убедиться, что при всех указанных обратных связях в результате структурных преобразований электромеханическую систему можно привести к виду, представленному на рис.8.44,а. Из рассмотрения этой обобщенной структуры следует, что при заданной механической части динамические свойства замкнутой системы регулирования определяются только передаточной функцией динамической жесткости механической характеристики bдинз(p). Так как применение общего метода синтеза системы по желаемой ЛАЧХ разомкнутого контура затруднено сложностью объекта регулирования, возможность анализа и синтеза по передаточной функции динамической жесткости для рассматриваемых объектов, представляет особый интерес.
Общая теория регулирования [ 11 ] и используемый в электроприводе инженерный метод последовательной коррекции свидетельствуют о том, что при любом сочетании обратных связей и любом способе коррекции при с12=¥ формируются статические характеристики и динамические свойства электропривода, в той или иной степени приближающиеся к настройкам либо на модульный, либо на симметричный оптимум. В этом легко убедиться, сопоставляя желаемую ЛАЧХ на рис.6.14 с ЛАЧХ на рис.6.18 и 6.19. При заданной механической части подобные ЛАЧХ для контура регулирования скорости в соответствии с рис.8.21,в могут быть получены путем формирования передаточной функции динамической жесткости bдинз(p) двух видов.
При статической системе регулирования скорости

При астатической

Выше выражения вида ( 8 142) были получены для разомкнутой системы (4.30), системы регулирования момента (7.29), скорости (8.28), (8.46) и (8.97). Аналогично (8.143) могут быть представлены динамические жесткости в различных системах астатического регулирования скорости- (8.35), (8.58), (8.97). Таким образом, формы (8.142) и (8 143) могут быть приняты в качестве эталонных для обобщенного представления множества конкретных регулируемых электроприводов, обобщенного анализа их свойств, синтеза и оптимизации по критерию минимума колебательности. Эталонные структуры для этого класса электроприводов, нормированные методом, изложенным в §4.6, представлены на рис.8 44,б и в. Характеристическое уравнение для обобщенного регулируемого электропривода со статическим регулированием скорости имеет четвертый порядок:

Если электромагнитная постоянная времени Тэ
пренебрежимо мала, динамические свойства упругой электромеханической системы при статическом регулировании скорости могут приближенно оцениваться уравнением третьей степени
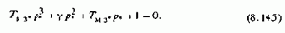
При переходе к астатическому регулированию порядок характеристического уравнения возрастает




Здесь:

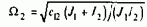

При этом показателем колебательности является логарифмический декремент l (4.36) или коэффициент затухания x (4.20) для той пары комплексно-сопряженных корней характеристического уравнения, которой соответствуют их меньшие значения. Эти показатели связаны между собой соотношением:

Для характеристических уравнений (8.144)-(8.146) составлены программы поиска с помощью цифровой ЭВМ максимальных значений l=lmax (x=xmax) при g=const и варьировании основных параметров электрической части системы. Таким образом для каждого характеристического уравнения получены обобщенные зависимости: lmax=f(TMA*) для уравнения (8.145); lmax=f(Tмз*·Тэз*). Для Уравнения (8.144); lmax= =f(Tм1з*·Тэз*·Тк*) для астатической системы регулирования (8.146). В качестве примера на рис.8.45,a представлены зависимости lmax=f(Tмз*·Тэз*) при g=const для статической системы регулирования.
Напомним, что Тм1з, обозначает электромеханическую постоянную времени первой массы, которая связана с электромеханической постоянной электропривода Tмз, соотношением
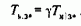
Использование этих кривых позволяет при заданном соотношении масс системы g определить значение (Tмз*·Tэз*)опт, оптимальное по критерию минимума колебательности, а затем по известному значению W12 выбрать удобно реализуемые значения (Tм1з)опт и (Tэз*)опт для

Таким путем были получены характеристики lпред=f(g) для всех рассматриваемых характеристических уравнений электромеханической системы, замкнутой по координатам первой массы, которые представлены на рис.8.45,б Эти кривые свидетельствуют о том, что электромагнитная инерционность расширяет возможности использования демпфирующей способности электропривода Действительно, при Тэ3»0 в статической системе регулирования критическое демпфирование (lпред=¥, xпред=1), можно реализовать лишь в электроприводах инерционных механизмов при g³9 (кривая 1).
В той же системе при оптимальной электромагнитной инерции Тэ3*=(Тэ3*)опт столь же высокое демпфирование достигается при g³5 (кривая 2). Наконец, в системе с астатическим регулированием критическое демпфирование обеспечивается при g³3
Известно, что индуктивность диссипативными свойствами не обладает, поэтому возможность увеличения с ее помощью демпфирующего действия электропривода требует разъяснений Двухмассовая упругая электромеханическая система объединяет в жестком взаимодействии две парциальные колебательные системы: весьма слабо демпфированную упругую механическую часть электропривода и двигатель, колебательность которого при жестких механических связях определяется соотношением электромагнитной и электромеханической постоянных времени Соответственно в АЧХ системы имеют место два резонансных пика. Оптимизация вызывает увеличение колебательности двигателя и снижение колебательности механической части, причем оптимум наступает при их равенстве Увеличение индуктивности приводит к увеличению колебательности двигателя, электромеханическая связь возрастает, увеличивая отвод энергии колебаний из механической части системы в электрическую. При этом предельное демпфирование наступает при меньшей механической инерционности, т. е. при меньших значениях g. Регулирование координат электропривода приводит к изменению динамической жесткости механической характеристики, чем расширяются возможности изменения соотношения постоянных времени Tм1з и Тэз и соответственно колебательности электрической парциальной системы. Дополнительные возможности, как следует из рассмотрения кривой 3 на рис.8.45,б, обеспечивает введение в закон регулирования скорости интегральной составляющей.
Исследования динамики упругих электромеханических систем рассматриваемого класса на цифровой ЭВМ дали исчерпывающие представления об их физических свойствах и послужили основой для достаточно эффективных методов расчетов. Тем не менее большой познавательный и практический интерес вызывают полученные в 80-х годах аналитические соотношения для определения оптимальных параметров электропривода.
Аналитические решения наглядно выявили и подтвердили уже известные взаимосвязи и соотношения параметров в оптимальных ситуациях, в ряде случаев помогли их правильнее понять и даже уточнить количественно.
В основе аналитических методов оптимизации лежит знание распределения корней характеристического уравнения при оптимальных параметрах системы. Исходные представления о распределении корней уравнения третьего порядка (8.145) дает диаграмма И. А Вышнеградского. Анализируя эту диаграмму, можно предположить, что предельному демпфированию при каждом g может соответствовать граничная кривая, определяющая равенство действительного корня p1=-a действительной части комплексно-сопряженных корней р23=-a ±jW, которое зависит в соответствии с (8.145) только от оптимального значения (Tмз*)опт=g(Tм1з*)опт. Воспользуемся этим предположением для получения аналитического метода оптимизации статической системы регулирования скорости при TЭЗ»0.
Указанное распределение корней позволяет разложить уравнение (8.145) на сомножители и представить в виде:

Перемножив сомножители, получим:

Приравнивание коэффициентов при одинаковых степенях в уравнениях (8.145) и (8.148а) позволяет получить систему уравнений

Решение этой системы дает следующие соотношения:

Сравним (8.150а) с графической зависимостью предельного демпфирования, полученной с помощью ЭВМ (кривая 1 на рис.8.45,б). Критическое демпфирование lпред=¥, xпред=1 наступает при g =9, результаты расчета lпред по (8.150а) и (8.147) при g>4 совпадают с кривой 1 на этом рисунке. Однако при g<4 штриховая линия 1', соответствующая (8.150а), существенно отклоняется от кривой 1, так как при g=3 значение xпред=0. Этот результат противоречит проведенному в гл.4 физическому анализу, поэтому решение требует уточнения. Очевидно, граничная кривая диаграммы Вышнеградского, принятая при разложении характеристического уравнения (8.145) на сомножители, определяет распределение корней, близкое к оптимальному в области 4<g<9, точно соответствует значению g=9 и недопустимо отклоняется от оптимального при g<4.
Поэтому представляет интерес разложение, при котором постоянная времени двучлена равна T1*

Корни этого уравнения в области значений g>6, где xпpед®1, близки корням (8.148а), а при g=9, где xпред=1, совпадает с ними. Аналогично (8.149а) получим:

Решение этой системы позволяет получить достоверные и удобные для оптимизации рассматриваемого электропривода по критерию минимума колебательности расчетные соотношения:

Расчет зависимости lпред=f(g) по (8.1506) и (8.147), а также зависимости (Tм1з*)опт=f(g) по (8.1516) дает значения, совпадающие с кривыми 1 и 1" соответственно, представленными на рис.8.45,б. При оптимизации значение (Tм1з*)опт, рассчитанное с помощью (8.1516), позволяет определить оптимальные параметры конкретного электропривода из условия

Увеличение порядка характеристического уравнения при учете Tэз* осложняет аналитическое решение задачи. Как выше отмечено, переход к уравнению (8.144) расширяет возможности оптимизации, варьирование Tмз* и TЭЗ* во многих случаях позволяет обеспечить высокое демпфирование путем реализации частных максимумов lmax, xmax, если по каким-либо причинам получение предельного демпфирования lпред, xпред затруднено (см. рис.8.45,а). Предельному демпфированию соответствует равенство колебательности электрической и механической парциальных систем, что определяет при lпред£¥ (xПред£1) равенство двух пар комплексно-сопряженных корней характеристического уравнения (8.144). Распределение корней при частных максимумах, соответствующих g=const, не столь однозначно, однако исследованиями на ЭВМ установлено, что в обширной области существенных значений TЭ3* им соответствует при этом же условии равной колебательности пропорциональность комплексно-сопряженных корней. В этой области при оптимальном сочетании параметров системы уравнение (8.144) может быть разложено на два сомножителя:

Нетрудно убедиться, что здесь корни первого и второго колебательного звена пропорциональны и имеют одинаковый коэффициент затухания.
Перемножив сомножители и приравняв полученные коэффициенты соответствующим коэффициентам уравнения (8.144), получим систему уравнений для определения оптимальных параметров электропривода:

Приравняв левые части второго и четвертого уравнений системы, получим
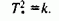
Тогда из первого уравнения системы (8.154) следует

С учетом этих соотношений третье уравнение системы примет вид:
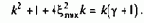
Так как
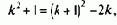
последнее уравнение представляется в виде:
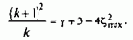
В то же время при полученных оптимальных соотношениях из четвертого уравнения системы следует

Приравнивая правые части этих уравнений, получаем биквадратное уравнение

Решение которого дает соотношение:

Знак «минус» в подкоренном выражении (8.157) определяется физическими соображениями. Известно, что при g®1 (J2®0) электромеханическая связь отсутствует, чему соответствует xmax®0. Так как при J2®0
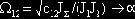
При оптимальных соотношениях параметров из третьего уравнения системы определяется коэффициент пропорциональности

Из уравнения (8.156) при известном значении k определяется

Далее из (8.155) получим

Анализ уравнения (8.157) свидетельствует о том, что разложение характеристического уравнения на сомножители (8.153) для частных максимумов справедливо лишь для значений

Предельному демпфированию lпред (xпрсд) соответствует k=1. Это значение k в (8.158) имеет место при
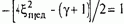
Отсюда

С помощью (8.159), (8.160) и (8.162) получаем следующие соотношения для определения оптимальных параметров, обеспечивающих предельное демпфирование:

Расчет зависимости lпред=f(g) по уравнениям (8.147) и (8.162) дает значения совпадающие с кривой 2 на рис.8.45,б, полученной с помощью ЭВМ. причем точное значение g=5, при котором обеспечивается критическое демпфирование lпред=¥ и xпред=1, было вначале получено аналитическим путем и затем подтверждено более тщательным поиском экстремума с помощью ЭВМ.
Формулы (8.162)-(8.164) просты и удобны для определения оптимальных параметров (Тэз)опт и (Тм3)опт, соответствующих предельному демпфированию.
Если эти параметры по каким-либо соображениям использовать нецелесообразно, с помощью соотношений (8.157)-(8.161) можно найти параметры, соответствующие при данном g частным максимумам демпфирования. Задавшись значением желаемой (Tэз*)опт из области (8.161), с помощью (8.157) определим реализуемый коэффициент затухания xmax и далее с помощью (8.160) оптимальное значение электромеханической постоянной времени.
Аналитическое решение задачи оптимизации системы с астатическим регулированием скорости, которой соответствует характеристическое уравнение пятого порядка (8.146), может быть получено аналогичным путем, если известно распределение корней, соответствующее оптимуму. Эта сложная задача для частных максимумов еще не получила удобного общего решения, поэтому ограничимся поиском параметров электропривода, обеспечивающих реализацию предельного демпфирования.
Из физических соображений предельному демпфированию в области до критического демпфирования (lпред£¥, xпред£1) должно соответствовать равенство комплексносопряженных корней характеристического уравнения, аналогично уравнению четвертого порядка. Это подтверждается исследованиями на цифровой ЭВМ, причем установлено, что пятый корень нормированного уравнения (8.146) при предельном демпфировании по абсолютной величине равен единице. Исходя из этих представлений о распределении корней, уравнение (8.146) при предельном демпфировании может быть разложено на следующие сомножители:

Путем приравнивания коэффициентов этого уравнения коэффициентам при тех же степенях p* в (8.146) получим:
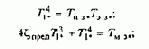

Вычитая из второго уравнения первое и из четвертого третье, получаем:

Затем вычтем (8.166) из (8.167), подставим в него выражение Tk* из пятого уравнения и определим Т1* как функцию соотношения масс g.

Следовательно,

Уравнение для определения зависимости xпpед=f(g) получим, подставив в третье уравнение исходной системы выражения (8.168)-(8 170):

Решение уравнения:

Знак «минус» в решении уравнения (8.172) опущен, так как дает отрицательные значения xпред, что лишено физического смысла.
Это решение, естественно, более громоздко, чем полученное выше для уравнения четвертого порядка, однако его анализ свидетельствует о том, что принятое распределение корней при разложении характеристического уравнения на множители (8.165) для предельного демпфирования достоверно. Так, подставив в (8.173) значение g®1, можно убедиться, что демпфирование при этом отсутствует, так как при весьма малых J2 электромеханическая связь с колебаниями второй массы нарушается, и вторая масса совершает недемпфированные колебания (естественным механическим демпфированием мы при математическом описании электромеханической системы пренебрегли). Увеличение J2 и g усиливает электромеханическую связь, колебания второй массы вызывают колебания скорости двигателя - соответственно демпфирование растет. При g=2,8 предельное демпфирование становится критическим, процессы в системе приобретают апериодический характер. Расчетная кривая lпред=f(g), полученная с помощью (8.147) и (8.173), достаточно близка к представленной на рис.8.45,б кривой 3, полученной при исследованиях динамики системы на математической модели, причем аналитический расчет позволяет незначительно уточнить значение у, при котором достигается критическое демпфирование.
Рассмотренный метод оптимизации электромеханической системы является разновидностью более общего широко используемого на практике метода так называемого модального управления электроприводами. Сочетание принципа синтеза по известному распределению полюсов передаточной функции замкнутой системы регулирования с выделением в структуре электромеханической системы передаточной функции динамической жесткости механических характеристик замкнутой системы bдинз(р), как показано, дает возможность определять оптимальные по критерию минимума колебательности параметры электрической части системы с помощью достаточно простых расчетных соотношений для широкого круга регулируемых электроприводов, разомкнутых по координатам М12, w2, ф2.
Выше было показано, что при демпфировании, близком к критическому, уменьшается быстродействие электропривода, и на этом основании использовалась настройка на технический (модульный) оптимум.Эту настройку дает возможность реализовать и рассмотренный метод оптимизации. Для этого необходимо задаться значением xопт=0,71 (lопт=6,28) и с помощью полученных аналитических соотношений определить соответствующие оптимальные значения относительных постоянных времени, затем выразить через них реальные параметры системы b3, Тмз, Тэз, Тк и определить параметры регуляторов, обеспечивающие получение требуемых передаточных функций динамической жесткости механических характеристик. В соответствии с кривыми на рис.8.45,б настройка на технический оптимум при Тэ»0 возможна лишь при g>5,5, при ТЭ¹0 при g>3, а в системе с астатическим регулированием скорости при g>1,8. При меньших g следует задаваться реализуемыми значениями lопт и xопт.