Автоматическое регулирование скорости в системе УП-Д


В результате преобразований (8.24) получим уравнение механической характеристики электропривода в виде

При р=0 уравнение (8.25) представляет собой уравнение статической механической характеристики


Чем выше коэффициент обратной связи koc, тем большее напряжение U3C требуется для получения той же скорости и тем меньше ошибка регулирования, обусловленная изменениями статической нагрузки. Статизм при данном коэффициенте обратной связи уменьшается с возрастанием коэффициента усиления k'n, и теоретически при k0ck'п®¥ статическая ошибка регулирования стремится к нулю.
Положив в (8.25) uзс=0, получим выражение динамической жесткости механической характеристики электропривода в замкнутой системе

где



При Тп>>Тэ уравнению (8.27) соответствуют частотные характеристики динамической жесткости,приведенные на рис.8.10,б. Увеличение коэффициента обратной связи по скорости при этом увеличивает модуль динамической жесткости только в низкочастотной области. При W>1/Тп модуль жесткости быстро уменьшается, и при W>1/Тпэ= =kуж/Тп асимптотическая ЛАЧХ сливается с такой же частотной характеристикой разомкнутой системы (kос=0).

С этой целью преобразуем структурную схему на рис.8.8 так, чтобы иметь одну единичную обратную связь по скорости (рис.8.11). Нетрудно видеть, что при этом связь момента с изменениями скорости при uзс=const определяется передаточной функцией - bдинзс(р) (8.27), что при жестком механическом звене определяет передаточную функцию разомкнутого контура регулирования в виде

При Tп=0 (8.29) запишем в виде

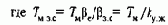
Частотные характеристики Lw(W), соответствующие (8.30), представлены на рис.8.10,в во взаимосвязи с ЛАЧХ динамической жесткости при Тп=0, показанными на рис.8.10,а. Увеличение коэффициента обратной связи kос приводит к увеличению bзс в диапазоне частот 0<W<1/Тэ, что влечет за собой смещение частоты среза W для системы при koc¹0 в область более высоких частот на участок с наклоном -40 дБ/дек.
Очевидно, это вызывает быстрое ухудшение динамических показателей качества регулирования. Фазочастотная характеристика электропривода Yw(Ф) при этом не зависит от koc, так как в разомкнутой и замкнутой системах фазочастотные характеристики динамической жесткости Yb(W) одинаковы (рис.8.10,a).
Вывод об увеличении колебательности вытекает непосредственно из рассмотрения (8.30), так как увеличение koc и kуж уменьшает Tмзс=TM/kуж. Отношение постоянных mзс=ТМЗС/ТЭ уменьшается, что и приводит к быстрому возрастанию колебательности. Малая постоянная времени быстродействующего преобразователя при этом является фактором, дополнительно снижающим запас по фазе на частоте среза, что ухудшает качество регулирования вплоть до возможной неустойчивости контура.
Большая постоянная времени преобразователя Тп>>Тэ, например, в системе Г-Д влияет на динамику регулирования несколько иначе. Частотные характеристики разомкнутого контура для этого случая показаны на рис.8.10,г, которые также следует сопоставить с соответствующими ЛАЧХ bдинзс (рис.8.10,б). Здесь при увеличении koc и kуж возрастает частота сопряжения 1/Тпэ, что вызывает сужение участка с наклоном -20 дБ/дек в области частоты среза, однако частота среза Wc в разомкнутой системе (koc=0) и в системе замкнутой по скорости (kос¹0), остается неизменной, пока 1/Тпэ<Wc. Следовательно, если средне-частотная асимптота в области частоты среза сохраняет достаточно протяженный участок с наклоном -20 дБ/дек, динамические свойства электропривода остаются близкими таковым в разомкнутой системе. Сравнивая фазо-частотные характеристики Yw(W) при kос=0 и koc¹Q (рис.8.10,в), можно убедиться, что при 1/Tпэ<<1/Тэ запас по фазе на частоте среза в замкнутой системе незначительно снижается по сравнению со снижением в разомкнутой системе, причем изменения определяются изменениями в зависимости Yb(W) (рис.8.10,б). Если при этом Тм>Тэ, можно определить допустимое по качеству регулирования значение koc, задавшись шириной среднечастотной асимптоты.
Например, при условии Тп'=4·Тэ допустимый коэффициент обратной связи по скорости составляет

Более точно это значение можно определить, задавшись требуемым запасом по фазе на частоте среза разомкнутого контура.
При kос>(kос)доп значения Тпэ приближаются к Тэ, участок с наклоном -20 дБ/дек сужается и исчезает, что соответствует неустойчивости контура регулирования. Таким образом, хотя при Тп>>Гэ возможности регулирования несколько расширяются, однако и в этом случае отрицательная связь по скорости увеличивает колебательность электропривода по сравнению с разомкнутой системой.
На основании проведенного анализа свойств электропривода, замкнутого отрицательной связью по скорости, можно заключить, что без применения динамической коррекции получить высокую точность регулирования при требуемых динамических показателях качества регулирования в большинстве случаев невозможно.
Стремление повысить точность регулирования, не прибегая к сложной динамической коррекции системы, определяет целесообразность использования комбинированного способа управления - дополнения системы регулирования по отклонению компенсацией возмущения, обусловленного нагрузкой. Из возможных реализаций компенсации рассмотрим случай, когда с этой целью используется жесткая положительная обратная связь по моменту двигателя, показанная на рис.8.8 штриховой линией. Такая обратная связь наиболее просто осуществляется в системе ТП-Д или Г-Д, где при Фном=const М=c·iя, т.е. достаточно ввести положительную связь по току якоря. Комбинированной системе регулирования соответствуют следующие уравнения, описывающие механическую характеристику электропривода:

В результате преобразований (8.32) при Uзс=0 с учетом (8.27) получим выражение динамической жесткости механической характеристики электропривода в такой системе в виде

Уравнение (8.33) свидетельствует о том, что введение положительной связи по моменту увеличивает модуль статической жесткости в замкнутой системе, причем при bеkпмk'п=1 модуль статической жесткости возрастает до бесконечности, а уравнение (8.33) принимает вид

При значительной инерционности преобразователя (Тп>>Тэ) уравнение (8.34) можно упростить:

Сравнивая (8.35) с (8.27), можно установить, что при этих условиях положительная связь по моменту (току) бесконечно увеличивает модуль статической жесткости (b'3с=¥ при W=0) и незначительно сказывается на показателях качества регулирования. Действительно, при построении асимптотических ЛАЧХ динамической жесткости, соответствующих (8.35) и (8.27), выявляется, что при W>l/Tп (8.27) приближенно выражается соотношением (8.35). Это значит, что среднечастотная асимптота разомкнутого контура регулирования скорости при введении положительной связи по моменту не претерпевает существенных изменений и динамические показатели комбинированной системы регулирования определяются коэффициентами усиления и отрицательной связи по скорости. Выбирая koc из условия (8.31) и устанавливая критическое значение коэффициента положительной связи по моменту из условия bekПMk'п=1, можно исключить статическую ошибку по нагрузке электропривода при сохранении показателей качества регулирования, соответствующих условию (8.31).
Таким образом, в системе Г-Д положительная связь по току при Тг» Тя является эффективным средством увеличения статической точности регулирования. Динамическая точность регулирования при этом возрастает незначительно, так как уже при небольших частотах (W>1/Гп) амплитудно-частотная характеристика |b'дин зc(fW)| практически совпадает с такой же характеристикой при kПM=0.
При высоком быстродействии преобразователя (Тп=0) увеличение жесткости механических характеристик за счет положительной связи по моменту ухудшает качество регулирования так же, как и при регулировании по отклонению. При этом требуемые точность и качество регулирования скорости достигаются применением параллельной или последовательной коррекции.
Как было установлено, при отсутствии коррекции частота среза Wc в замкнутой системе при больших Тп остается близкой частоте среза при kос=0, которая определяется соотношением Wс=1/mТэ, при этом быстродействие электропривода по нагрузке определяется электромагнитной инерцией силовой цепи (Тэ) и отношением постоянных m=ТМ/ТЭ.
Объясняется это тем, что при высоких частотах большая постоянная Тп для внешней обратной связи по скорости является фильтром и свойства электропривода определяются внутренней, а не внешней обратной связью по скорости.
Быстродействие электропривода по управляющему воздействию зависит от Тп и koc. В этом можно убедиться, рассматривая структурную схему на рис.8.11. При скачке U3C скорость w0зс изменяется тем быстрее, чем меньше Тп и чем сильнее отрицательная обратная связь по скорости. В соответствии с уравнением
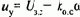
отрицательная связь по скорости оказывает форсирующее действие на замедленные инерцией преобразователя процессы: чем больше koc, тем больше при заданной скорости скачок U3C и начальное значение uy что при надлежащем запасе по напряжению управления преобразователя (uв в системе Г-Д) обеспечивает увеличение темпа изменения w0 и ускорение протекания переходных процессов.
