Автоматы для регулярных языков

Покажем, что каждый регулярный язык можно распознать конечным автоматом.

Теорема 5.1. Для каждого регулярного выражения r можно эффективно построить такой недетерминированный конечный автомат M, который распознает язык, задаваемый r, т.е. LM= Lr.

Доказательство Построение автомата M по выражению r проведем индукцией по длине r, т.е. по общему количеству символов алфавита ?, символов

и ?, знаков операций +, ?, * и скобок в записи r.

Базис. Автоматы для выражений длины 1:

, ? и a

? показаны на следующем рисунке.

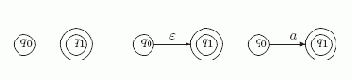
Рис. 5.1.

Заметим, что у каждого из этих трех автоматов множество заключительных состояний состоит из одного состояния.

Индукционный шаг. Предположим теперь, что для каждого регулярного выражения длины

k построен соответствующий НКА, причем у него единственное заключительное состояние. Рассмотрим произвольное регулярное выражение r длины k+1. В зависимости от последней операции оно может иметь один из трех видов: (r1 + r2), (r1 r2) или (r1)*. Пусть M1= <?, Q1, q01, {qf1}, ?1 > и M2= <?, Q2, q02, {qf2}, ?2 > - это НКА, распознающие языки Lr1 и Lr2, соответственно. Не ограничивая общности, мы будем предполагать, что у них разные состояния: Q1

Q2 =

Тогда НКА M= <?, Q, q0, {qf}, ? >, диаграмма которого представлена на рис. 5.2, распознает язык Lr =Lr1 + r2=Lr1

Lr2.

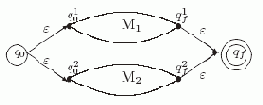
Рис. 5.2.

У этого автомата множество состояний Q = Q1

{ q0, qf}, где q0 - это новое начальное состояние, qf - новое (единственное !) заключительное состояние, а программа включает программы автоматов M1 и M2 и четыре новых команды ?-переходов: ? = ?1

{q0

q01, q0

q02, qf1

qf, qf2

qf}. Очевидно, что язык, распознаваемый НКА M, включает все слова из L{M1} и из L{M2}. С другой стороны, каждое слово w

LM переводит q0 в qf, и после первого шага несущий его путь проходит через q01 или q02. Так как состояния M1 и M2 не пересекаются, то в первом случае этот путь может попасть в qf только по ?-переходу из qf1 и тогда w

LM1}. Аналогично, во втором случае w

LM2.

Для выражения r = r1? r2 диаграмма НКА M= <?, Q, q0, {qf}, ? >, распознающего язык Lr, представлена на следующем рисунке.

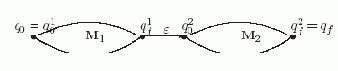
Рис. 5.3.

У этого автомата множество состояний Q = Q1

Q2 , начальное состояние q0= q01, заключительное состояние qf =qf2, а программа включает программы автоматов M1 и M2 и одну новую команду - ?-переход из заключительного состояния M1

в начальное состояние M2, т.е. ? = ?1

{ qf1

q02}. Здесь также очевидно, что всякий путь из q0= q01 в qf =qf2 проходит через ?-переход из qf1 в q02. Поэтому всякое слово, допускаемое M, представляет конкатенацию некоторого слова из LM1} с некоторым словом из LM2}, и любая конкатенация таких слов допускается. Следовательно, НКА M распознает язык Lr =L r1 ? r2}=L r1 Lr2.

Пусть r = r1*. Диаграмма НКА M= <?, Q, q0, {qf}, ? >, распознающего язык Lr=Lr1* = LM1*

представлена на рис. 5.3.

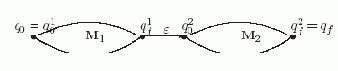
Рис. 5.3. Диаграмма автомата M, распознающего язык Lr1*

У этого автомата множество состояний Q = Q1

{ q0, qf}, где q0 - это новое начальное состояние, qf - новое (единственное !) заключительное состояние, а программа включает программу автомата M1 и четыре новых команды ?-переходов: ? = ?1

{q0

q01, q0

qf, qf1

q01, qf1

qf}. Очевидно, ?

LM. Для непустого слова w по определению итерации w

Lr1*

для некоторого k

1 слово w можно разбить на k подслов: w=w1w2… wk и все wi

LM1. Для каждого i= 1,… ,k слово wi переводит q01 в qf1. Тогда для слова w в диаграмме M имеется путь

Следовательно, w

LM. Обратно, если некоторое слово переводит q0 в qf, то либо оно есть ? , либо его несет путь, который, перейдя из q0 в q01 и затем пройдя несколько раз по пути из q01 в qf1 и вернувшись из qf1 в q01 по ?-переходу, в конце концов из qf1 по ?-переходу завершается в qf. Поэтому такое слово w

L M1*.

Из теорем 4.2 и 5.1 непосредственно получаем

Следствие 5.1.

Для каждого регулярного выражения можно эффективно построить детерминированный конечный автомат, который распознает язык, представляемый этим выражением.

Это утверждение - один из примеров теорем синтеза: по описанию задания (языка как регулярного выражения) эффективно строится программа (ДКА), его выполняющая.

Справедливо и обратное утверждение - теорема анализа.

Теорема 5.2.

По каждому детерминированному ( или недетерминированному) конечному автомату можно построить регулярное выражение, которое представляет язык, распознаваемый этим автоматом.

Доказательство этой теоремы достаточно техническое и выходит за рамки нашего курса.

Таким образом, можно сделать вывод, что класс конечно автоматных языков совпадает с классом регулярных языков. Далее мы будем называть его просто классом автоматных языков.

Автомат Mr, который строится в доказательстве теоремы 5.1 по регулярному выражению r, не всегда является самым простым.

Например, для реализации выражения-слова a1a2 … an, где ai

? (i=1,2, … , n), можно просто использовать автомат с (n+1) состоянием qi (i=0,1,2, … , n) и командами q{i-1} ai

qi, в котором нет пустых ?-переходов, участвующих в общей конструкции для конкатенации. Также при построении автомата для объединения M1 и M2 можно сливать их начальные состояния в одно, если в них нет переходов из других состояний (тогда не потребуется новое начальное состояние). Можно также объединить их заключительные состояния, если из них нет переходов в другие состояния и алфавиты M1 и M2 совпадают. Если из заключительного состояния M1 нет переходов в другие состояния, то при конкатенации его можно объединить с начальным состоянием M2. Вместе с тем, утверждения задачи 5.9 показывают, что наша общая конструкция достаточно экономна.

Пример 5.7. Применим теорему 5.1 к регулярному выражению r = (1 +01 +001)*(? + 0 +00), которое, как мы заметили в примере 5.4, представляет язык, состоящий из всех слов, которые не содержат подслово '000'.

На рис. 5.5 представлены диаграммы автоматов M1 и M2, построенных по выражениям r1 = (1 +01 +001) и r2= (? + 0 +00), соответственно, с помощью конструкций для конкатенации и объединения. Как мы отмечали выше, автомат M1 можно было бы еще упростить, склеив начальные состояния q2, p1 и s1, а также заключительные состояния q3, p3 и s4.

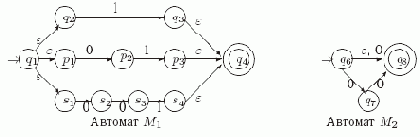
Рис. 5.5.

Автомат M3 для выражения r1* = (1 +01 +001)* получается из M1 добавлением нового начального состояния q0 и заключительного состояния q5 и ?-переходов из q0 в q1 и q5, из q4 в q5 и из q5 в q1.Затем результирующий автомат для исходного выражения r получается последовательным соединением M3 и M2. Он представлен ниже на рис. 5.6.

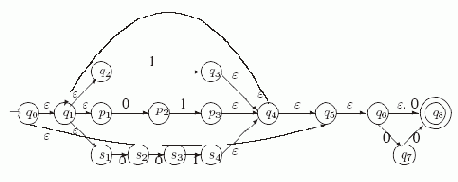
Рис. 5.6.

Содержание раздела