Переработка информации с помощью конечных автоматов

Конечные автоматы являются математической моделью устройств, перерабатывающих дискретную входную информацию в режиме "реального времени", т.е. в темпе ее поступления.

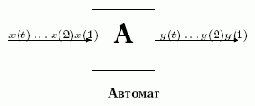
Автомат

На такие устройства в последовательные дискретные моменты времени 1,2, …, t, t+1,… поступают входные сигналы x(1),x(2), …, x(t),x(t+1),… и в ответ на них автомат A вырабатывает выходные сигналы y(1) y(2), …, y(t), y(t+1),…. Конечные автоматы характеризуются двумя особенностями.

Отсутствие предвосхищения: выходной сигнал y(t), выдаваемый автоматом в момент t, зависит лишь от полученных к этому времени входов x(1),x(2), …, x(t), т.е. автомат не может предвосхитить будущие входы и заранее на них отреагировать. Таким образом, имеется некоторая функция выходов
(x(1),x(2), …, x(t))= y(t), определяющая очередной выход по предшествующему входу.
Конечная память: в каждый момент t информация в автомате о полученном к этому моменту входе x(1),x(2), …, x(t) конечна. Это свойство удобно интерпретировать следующим образом: автомат имеет конечное множество состояний Q и в каждый момент находится в одном из этих состояний. При получении очередного входа состояние может измениться. Таким образом, состояние q
Q, в котором находится автомат после получения входной последовательности x(1),x(2), …, x(t), и представляет информацию об этой последовательности, используемую в дальнейшей работе автомата при определении следующего состояния и выхода.

Наше обсуждение приводит к следующему определению конечного автомата с выходом.

Определение 4.1. Конечный автомат - преобразователь - это система вида

включающая следующие компоненты:

?X={a1, … , am} (m
1) - конечное множество - входной алфавит;
?Y={b1, … , br} (r
1) - конечное множество - выходной алфавит;
Q={q0, … , qn-1} (n
1) - конечное множество - алфавит внутренних состояний;
q0
Q - начальное состояние автомата;
?: Q ? ?X
Q - функция переходов, ?(q, a) - это состояние, в которое переходит автомат из состояния q, когда получает на вход символ a;
: Q ? ?X
?Y - функция выходов,
(q, a) - это символ из ?Y, который выдает на выход автомат в состоянии q, когда получает на вход символ a.

Иногда пару функций ?,

называют программой автомата A и задают как список из m n команд вида qiaj

?(qi,aj) /

(qi,aj).

Другой удобный способ задания функций ? и

- табличный. Каждая из них определяется таблицей (матрицей) размера n ? m, строки которой соответствуют состояниям из Q, а столбцы - символам из входного алфавита ?X. В первой из них на пересечении строки qi и столбца aj стоит состояние ?(qi,aj), а во второй - выходной символ

(qi,aj).

Еще один способ представления конечного автомата основан на использовании ориентированных размеченных графов.

Определение 4.2. Диаграмма автомата A = <?X, ?Y, Q, q0, ?,

> - это ориентированный (мульти) граф DA=(Q, E) с помеченными ребрами, в котором выделена вершина-начальное состояние q0 и из каждой вершины q

Q выходит |?X| ребер, помеченных парами символов a / b (a

?X, b

?Y). Таким образом, для каждой q

Q и каждого символа a

?X имеется единственное ребро с меткой a /

(q,a) из q в вершину q' =?(q,a).

Как автомат A перерабатывает входное слово x1x2 … xt? Он начинает работу в состоянии q(0)=q0. Затем, получив (прочитав) входной символ x1, переходит в состояние q(1)= ?(q0,x1) и выдает символ y(1)=

(q0,x1). Далее, получив x2 A переходит в состояние q(2)= ?(q(1),x2) и выдает символ y(2)=

(q(1),x2) и т.д. Таким образом, работа автомата, характеризуется последовательностью проходимых им состояний q(0), q(1), … , q(t), … и последовательностью выходных символов y(1), … , y(t), … . Они определяются следующими реккурентными соотношениями:

Рассмотрим несколько примеров автоматов-преобразователей.

Пример 4.1. Сумматор последовательного действия

Мы уже строили схему из функциональных элементов SUMn, реализующую для фиксированного n суммирование двух n-разрядных двоичных чисел. Построим теперь конечный автомат SUM, который сможет складывать два двоичных числа произвольной разрядности. На вход этого автомата будут последовательно подаваться пары x(i)= (x1(i),x2(i)) соответствующих i-ых (1

r) разрядов двух двоичных чисел x1=x1(r) … x1(2) x1(1) и x2=x2(r) … x2(2) x2(1), а признаком завершения чисел будет служить символ x(r+1)= * (если одно из слагаемых короче другого, то будем считать, что недостающие разряды - нули).

Выходом автомата должна быть последовательность (r+1) двоичных разрядов суммы y = x1 + x2:

Таким образом, входной алфавит автомата: ?X ={ (00), (01), (10), (11), *}, а выходной алфавит: ?Y={ 0, 1}. Что нужно знать автомату SUM о первых i разрядах x1 и x2, чтобы получив их (i+1)-ые разряды (x1(i+1),x2(i+1)), верно определить выход y(i+1)? Ясно, что для этого достаточно знать, был ли перенос в i-ый разряд. Поэтому можно зафиксировать множество состояний Q = {q0, q1}, в котором q0 означает, что переноса не было, а q1 - что перенос был. Теперь легко построить таблицы, представляющие функции переходов и выходов автомата SUM.

?:Q\?X

(00)(01)(10)(11)*?:Q\?X(00)(01)(10)(11)*

q0	q0	q0	q0	q1	q0
q1	q0	q1	q1	q1	q0
q0	0	1	1	0	0
q1	1	0	0	1	1

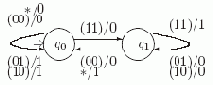
Заметим, что после получения символа * автомат SUM переходит в начальное состояние q0 и готов выполнять сложение следующей пары чисел.

Рис. 4.1. Диаграмма автомата SUM

На диаграмме автомата у вершины q0 четыре петли, а у вершины q1 - три, объединены в одну с четырьмя и тремя метками, соответственно. Точно так же слиты два ребра из q1 в q0. Стрелкой указано начальное состояние.

Содержание раздела