Лекции ТММ
         

Понятие о геометрических и кинематических характеристиках механизмов




 		ЛЕКЦИЯ 3

    Краткое содержание: Понятие о геометрических и кинематических характеристиках механизмов (функция положения и ее производные по времени и по обобщенной координате). Методы определения геометро-кинематических характеристик механизма. Цикл и цикловые графики. Связь между кинематическими и геометрическими параметрами. Кинематическое исследование типовых механизмов: рычажных, зубчатых, кулачковых, манипуляторов.


Понятие о геометрических и кинематических характеристиках механизмов.

    Функцией положения механизма называется зависимость углового или линейного перемещения точки или звена механизма от времени или обобщенной координаты.

Геометрические и кинематические характеристики механизма
Рис. 3.1

    Кинематическими передаточными функциями механизма называются производные от функции положения по обобщенной координате. Первая производная называется первой передаточной функцией или аналогом скорости (обозначается Vq,wq), вторая - второй передаточной функцией или аналогом ускорения (обозначается aq, eq).

    Кинематическими характеристиками механизма называются производные от функции положения по времени. Первая производная называется скоростью (обозначается V, w), вторая - ускорением (обозначается a, e).

    Механизм с одной подвижностью имеет одно заданное входное движение и бесчисленное множество выходных ( движение любого звена или точки механизма ). Передаточные функции тех движений, которые в данном случае используются как выходные, называются главными, остальные - вспомогательными.

    Рассмотрим схему механической системы образованной последовательно-параллельным соединением типовых механизмов. Схема включает входное звено, зубчатую передачу , кулачковый и рычажный механизмы и имеет два выходных звена.

Схема механической системы
Рис. 3.2

Рис. 3.3

Функции положения в механизмах
Рис. 3.4

Методы геометро-кинематического исследования механизмов

  • планов положений, скоростей и ускорений,
  • проекций векторного контура,
  • кинематических диаграмм,
  • центроид,
  • преобразования координат,
  • экспериментальный,
  • другие.

Связь кинематических и передаточных функций


    Линейные скорости и ускорения

    VL= dSL / dt = (dSL / df1) * (df1 / dt) = VqL * w1;

    a L = d(Vql * w1) / dt = (dVqL / df1) * (df1 / dt) * w1 + Vql * e1 = aqL * w12 + VqL * e1;

    Угловые скорости и ускорения

    wi = dfi / dt = (dfi / df1) * (df1 / dt) = wqi * w1;

    ei = d(wqi * w1) / dt = (dwi / df1) * (df1 / dt) * w1 + wqi * e1 = eqi * w12 + wqi * ei.

    Так как данные формулы получены как производные от скалярных величин, то при операциях с векторными величинами они применимы только для проекций этих величин на оси координат.

    1. Метод проекций векторного контура. (Рычажные механизмы).

Рассмотрим простейший кулисный механизм.
Рис. 3.5

    Заменим кинематическую схему механизма эквивалентным векторным контуром

    Тогда уравнение замкнутости векторного контура запишется:

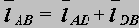    1. 1. Задача о положениях звеньев механизма
Рис. 3.6

    Проецируем векторный контур на оси координат и получаем координаты точки В механизма:

    xB = lAB * cos (f1) = lAD * cos (p) + lDB * cos (f3);

    yB = lAB * sin (f1) = lAD * sin (p) + lDB * sin (f3);

из решения этой системы уравнений определяем неизвестные величины f3 и lDB, которые определяют положение звеньев и точек механизма

    tg (f3 ) = sin (f3) / cos (f3) = lAB * sin (f1) / (lAB * cos (f1) - lAD * cos (p));

    lDB = (lAB * sin (f1) / sin (f3);

    1. 2. Задача о первых кинематических передаточных функциях механизма

    Продифференцируем уравнения проекций векторного контура по обобщенной координате и получим

    VqBx = -lAB * sin (f1) = VqDB * cos (f3) - lDB * wq3 * sin (f3);

    VqBy = lAB * cos (f1) = VqDB * sin (f3) + lDB * wq3 * cos (f3).

Из этой системы уравнений определяем первые передаточные функции VqB и wq3.

    1. 3. Задача о вторых передаточных функциях механизма.

    Вторично продифференцируем уравнения проекций векторного контура по обобщенной координате и получим



    aqBx = -lAB * cos (f1) = aqDB * cos (f3) - 2 * VqDB * w3 * sin (f3) - lDB * eq3 * sin (f3) - lDB*
    * w32 * cos (f3);

    aqBy = -lAB * sin (f1) = aqDB * sin (f3) + 2 * VqDB * w3 * cos (f3) + lDB * eq3 * cos (f3) - lDB *
    * w32 * sin (f3);

Из этой системы уравнений определяем вторые передаточные функции aqB и eq3.

        Цикловые кинематические (геометрические) диаграммы для кулисного механизма.

   Циклом называется период времени или изменения обобщенной координаты по истечении которого все параметры системы принимают первоначальные значения.

   Поэтому значения величин в начале и в конце цикла одинаковы.

Рис. 3.7

Метод центроид (Зубчатые передачи).

    Центроидой (полоидой) называется геометрическое место центров (полюсов) относительного вращения в системах координат связанных со звеньями механизма. В зубчатом механизме при передаче движения центроиды колес перекатываются друг по другу без скольжения.

Схема зубчатого механизма
Рис. 3.8

    Повернем ведущее колесо на малый угол df1, тогда ведомое колеса повернется на угол df1.Так как центроиды или начальные окружности колес перекатываются друг по другу без скольжения , то дуга dSw1будет равна дуге dSw2. Тогда можно записать следующее равенство:

dSw1 = dSw2 = dSw,

где: dSw1 = rw1 * df1, dSw2 = rw2 df2.

Откуда: u21 = df2 / df1 = rw1 / rw2 = const.

Функция положения для выходного звена зубчатой передачи

Вторая передаточная функция для выходного звена зубчатой передачи

eq2 = dU21 / df1 = 0.

    Механизм зубчатой передачи не является цикловым механизмом, так как угловое перемещение выходного звена увеличивается при увеличении углового перемещения входного. Поэтому кинематические диаграммы построим только для одного оборота входного звена.

        Диаграммы функции положения и передаточных функций для зубчатой передачи.

   3. Метод цикловых кинематических диаграмм (кулачковые механизмы).

   Кулачковым называется трехзвенный механизм состоящий из двух подвижных звеньев - кулачка и толкателя, соединенных между собой высшей кинематической парой. Часто в состав механизма входит третье подвижное звено - ролик, введенное в состав механизма с целью замены в высшей паре трения скольжения трением качения. При этом механизм имеет две подвижности одну основную и одну местную (подвижность ролика).    Основные параметры кулачкового механизма:

fраб - фазовый рабочий угол кулачкового механизма;

fраб = dраб = fc + fдв + fу;
fс - угол сближения;
fдв - фазовый угол дальнего выстоя;
fу - фазовый угол удаления;
dраб - профильный рабочий угол;
fбв - угол ближнего выстоя;
hBm - максимальное перемещение точки В толкателя;
r0 - радиус начальной шайбы кулачка;
rр - радиус ролика.

Рис. 3.9




Рис. 3.10

Рис. 3.11

    При кинематическом анализе кулачкового механизма задан конструктивный профиль кулачка и радиус ролика rp. Методом обращенного движения (перекатывая ролик по неподвижному конструктивному профилю кулачка) находим центровой профиль кулачка (траекторию центра ролика толкателя в обращенном движении). Наносим на профиль фазовые углы и определяем в зоне ближнего выстоя начальный радиус центрового профиля кулачка r0. В зоне рабочего угла проводим ряд траекторий центра ролика толкателя (точки В) и по ним измеряем от точки лежащей на окружности r0 до точки лежащей на центровом профиле текущее перемещение толкателя SBi. По этим перемещениям строим диаграмму SB = f(f1). Дифференцируя эту диаграмму по времени или обобщенной координате получаем кинематические или геометрические характеристики механизма. При графическом дифференцировании масштабы диаграмм зависят от масштабов исходной диаграммы и выбранных отрезков дифференцирования:

mS = yhb / hB мм/м;     mf = b / fр мм/рад;     mt = b/tрмм/с;

mVq = k1 * mS / mf мм/м;     maq = k2 * mVq / mf мм/м;

mV = k1 * mS / mt мм/м*с-1;     ma = k2 * mV / mtмм/м*c-2;

где b - база диаграммы по оси абсцисс в мм, yhB - ордината максимального перемещения толкателя в мм, hB - максимальное перемещение толкателя в м, tр - время поворота кулачка на фазовый угол fрв с, k1 и k2 - отрезки дифференцирования в мм.

4. Метод преобразования координат (Манипуляторы)

    При использовании метода преобразования координат задача о положении выходного звена решается путем перехода из системы в которой это положение известно в систему в которой его требуется определить. Переход от системы к системе осуществляется перемножением матриц перехода в соответствующей последовательности.

   4. 1. Формирование матрицы перехода для плоских механизмов.
Рис. 3.12
   Координаты точки М в системе i через координаты этой точки в системе j определятся следующей системой уравнений:

Тогда векторы столбцы координат точки М и матрица перехода из системы j в систему i

Векторное уравнение перехода из системы j в систему i

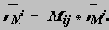Пример применения метода преобразования координат для плоского трехподвижного манипулятора:
Рис. 3.13


5. Экспериментальный метод кинематического исследования.

    При экспериментальном исследовании кинематики механизмов кинематические характеристики звеньев и точек механизма определяются и регистрируются с помощью чувствительных элементов - датчиков, которые используя различные физические эффекты преобразуют кинематические параметры в пропорциональные электрические сигналы. Эти сигналы регистрируются измерительными самопишущими приборами (самописцами, осциллографами и др.). В последнее время для регистрации и обработки экспериментальных данных все более широко используются специальные или универсальные компьютеры. Для примера рассмотрим экспериментальную установку для исследования кинематических характеристик синусного механизма:
Рис. 3.14
В этой экспериментальной установке:

  • для измерения перемещения выходного звена используется потенциометрический датчик перемещения, в котором пропорционально положению движка потенциометра изменяется его сопротивление;

  • для измерения скорости выходного звена используется идукционный датчик скорости, в котором напряжение на концах катушки движущейся в поле постоянного магнита пропорционально скорости катушки;

  • для измерения ускорения выходного звена используется тензометрическиий акселерометр. Он состоит из пластинчатой пружины один конец которой закреплен на выходном звене механизма, а на втором закреплена масса. На пластину наклеены проволочные тензопреобразователи. При движении выходного звена с ускорением инерционность массы вызывает изгиб пластины , деформацию тензопреобразователей и изменение их сопротивления пропорциональное ускорению выходного звена.

Передаточные функции механизмов с несколькими подвижностями (W>1).

Рассмотрим простой двухподвижный манипулятор
Рис. 3.15
Функция положения для выходного звена этого механизма является функцией двух переменных

f2 = P(f10,f21),

и ее производная определится как производная функции двух переменных:

df2 = [dP(f10,f21) / df10] df10 + [dP(f10,f21) / df21] df21 = wq10 * df10 + wq21 * df21,

где wq10 и wq21 - частные производные по обобщенным координатам.


Содержание раздела